近年、深層学習の登場によって、画像認識などのパターン認識技術の精度は、飛躍的に向上しています。高い精度を達成するには、大量データを学習する必要がありますが、実問題への適用を考えた場合、そのような大量データを準備することは難しい場合が多く、限られたデータでどう精度を高めるかが課題となっています。本稿では、少量の学習データに対して効果的な深層学習を行うために開発した、2つの技術を紹介します。1つは、深層ネットワークの構造に基づき、層ごとに異なる正則化の強さを適切に設定する「層ごとの適応的正則化」、もう1つは、中間層で識別が難しい苦手な特徴を生成しながら学習する「敵対的特徴生成」です。手書き数字認識や一般物体認識の公開データセットに対する実験をとおして、その有効性を明らかにします。

1. はじめに

近年、深層学習の登場により、画像認識などのパターン認識技術の精度は飛躍的に向上しています。深層学習によって高い認識精度を得るには、入力するパターンとそれに対する正解値からなる学習データを、少なくとも数千件から数万件、大量に準備する必要があります。しかし、実問題への適用を考えた場合、そのような大量の学習データを準備することは、さまざまな要因で難しいことが多いです。例えば、発生頻度の低い異常データはデータ収集に長い期間を要しますし、医療データは専門医でないと正解が分かりません。また、迅速なサービスインのために、大量の学習データを構築する時間がとれない場合もあります。このような理由から、少量の学習データからでもいかに高い精度を実現するかが、深層学習技術の実応用を広げるうえで、非常に重要な課題となっています。

学習データが少量の場合、学習するデータに過剰に適合し、学習していないデータに対する精度が低下する、過学習と呼ばれる現象が顕著になります。通常の深層学習では、深層ネットワークの重みパラメータの二乗和が小さくなるように制約を加える正則化によって、過学習を軽減しています。しかし、正則化が強すぎて学習が進まない層と、正則化が弱すぎて過学習となる層が混在し、精度改善は限定的という問題がありました。また、画像を回転させたり大きさを変えたりして擬似的にデータを増やす、データ拡張と呼ぶ手法がよく用いられますが、必ずしも精度改善に寄与するデータが作れないという問題がありました。

本稿では、少量データを学習する際に生じる前述した問題を解決し効果的な深層学習を行うために開発した、層ごとの適応的正則化と、敵対的特徴生成について紹介します。また、手書き数字認識や一般物体認識の公開データを用いた評価実験によって、これらの有効性を明らかにします。

2. 層ごとの適応的正則化

2.1 深層学習と過学習

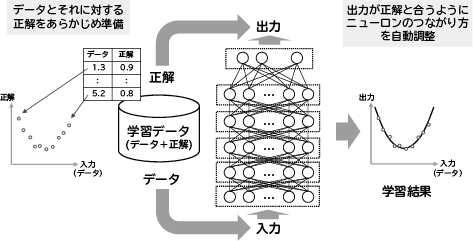
深層学習の仕組みについて、簡単に説明します（図1）。まず、データとそれに対する正解からなる学習データを、あらかじめ準備しておきます。次に、データを入力した時に得られるネットワークの出力が、その正解と合うようにニューロンのつながり方を調整します。これを学習と呼び、すべての学習データに対して、出力と正解の誤差が十分小さくなった時点で学習を終了します。

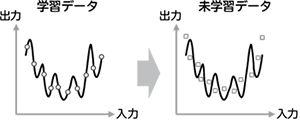
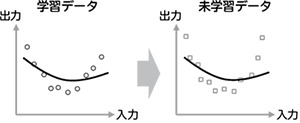
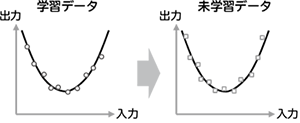
学習データが少ない場合、学習データに含まれるノイズにまで過剰に適合し、学習していない未学習データに対する精度が低下する、過学習と呼ぶ現象が顕著になります（図2）。これを軽減するため、従来よりL2正則化と呼ばれる手法が用いられています。L2正則化では、正解と出力の誤差だけでなく、学習するパラメータ（深層学習では結合重み）の2乗の総和も同時に最小化します。これにより、パラメータの値が過度に大きくなることを防ぎ、過学習を軽減します。しかし、逆に正則化が強すぎると学習が進まなくなり、データに対する適合性が低下します（図3）。したがって、高い精度を得るには、正則化の強さを適切に設定することがとても重要です（図4）。

2.2 従来のL2正則化の問題点

深層学習は、深い層構造を持つニューラルネットワークの学習方法であり、出力と正解の誤差をそれより前の層に伝播させながら、各層の結合重みを更新します。これは、誤差逆伝播法と呼ばれ、i層目の結合重みをw_iとし、誤差逆伝播法で算出したw_iに対する勾配をΔw_iとすると、

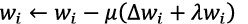
と更新します。ここで、μは更新の大きさを決める学習率、λはL2正則化の強さを決める正則化係数です。Δw_iは出力と正解の誤差が小さくなるように学習を進めるアクセルとして作用し、λw_iはそれを抑えるブレーキとして作用するので、適切な正則化の効果を得るには、Δw_iとλw_iがうまくバランスするようにλの値を設定する必要があります。

誤差逆伝播法で算出されるΔw_iは、i層目より後段のネットワーク構造に応じて伝播される大きさが変わります。一方、λw_iはi層目の結合重みのみに依存してその大きさが決まるので、この2つの大きさのバランスは、層ごとに異なります。ところが、従来の深層学習では、すべての層で同じλを用いるため、層ごとに2つの大きさのバランスが変わり、正則化が強すぎる層や弱すぎる層が混在してしまいます。層が深くなるほどこの問題は深刻になります（図5）。

2.3 層ごとの適応的正則化

この問題を解決するため、層ごとに異なる正則化係数を適切に決定する、層ごとの適応的正則化と呼ぶ技術を開発しました。本技術では、勾配と正則化項の大きさの比率が一定となるように正則化係数を決めます。i層の正則化係数をλ_iと表記すると、

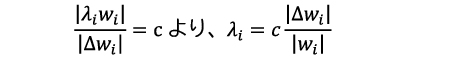
となります。cは層に依らない定数です。しかし、学習前は勾配の大きさ︱Δw_i︱が分からないので、λ_iを直接求めることはできません。そこで、隣り合う層との勾配の大きさの比を推定し、この比に基づいて正則化係数の比を推定します。したがって、最終層の正則化係数が決まれば、求めた比に応じて他の層の正則化係数を自動的かつ適切に決めることができます（図6）。調整が必要なのは最終層の正則化係数のみであり、従来のL2正則化と同様の手間で、層ごとに適応的に正則化係数を決定できます¹⁾。

2.4 実験

本技術の有効性を評価するため、手書き数字データセットMNISTを用いた実験で、従来のL2正則化と認識精度を比較しました（図7）。横軸は学習データ数、縦軸はテストデータに対するエラー率です。従来に比べエラーを2割近く削減できており、本技術の効果が確認できました。

3. 敵対的特徴生成

3.1 従来のデータ拡張

画像認識では、画像が多少変形しても、画像に写っているモノの意味は変わりません。そこで、画像を回転させたり大きさを変えたりして人工的にデータを増やす、データ拡張と呼ばれる手法が、深層学習ではよく用いられます。

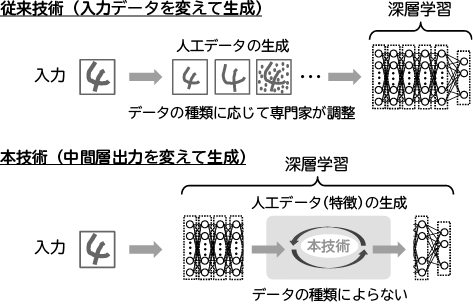
認識精度の向上には、認識が難しいデータをより多く学習することが有効ですが、データ拡張ではそのようなデータが生成されるとは限らず、精度改善は限定的でした。また、画像や音声などデータの種類に応じて、生成したデータが悪影響を及ぼさないように、専門家がデータの生成方法を調整する必要がありました（図8）。

3.2 敵対的特徴生成

この問題を解決するため、深層ネットワークの中間層で得られる特徴量を意図的に変化させることで、認識が難しい学習データを人工生成する、敵対的特徴生成と呼ぶ技術を開発しました。ランダムに選択した中間層の出力をh、それに対するネットワークの出力をg(h)と書くと、

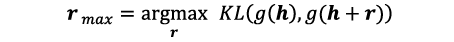
として特徴hに付加する摂動r_maxを生成します。ここで、KLはカルバック・ライブラー・ダイバージェンスと呼ばれ、2つの値が似ているほど小さくなります。これが大きくなるようなrを求めるということは、特徴h+rに対する出力g(h+r)が、摂動を付加する前の出力g(h)と大きく変わることを意味します。出力が大きく変わるデータは、認識が難しいデータなので、得られたh+r_maxを敵対的特徴と呼びます。ただし、rの大きさに何の制約も付けないと、悪影響を及ぼす摂動を作ってしまうので、

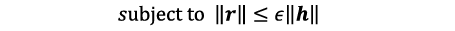
という制約付きでr_maxを求めます。ここで、ε>0はrの大きさを規定するパラメータで、あらかじめ設定しておきます。学習データを入力するたびに、それに応じた敵対的特徴が次々と生成されるので、これらを正しく認識するように学習することで、認識精度が向上します^2）。

従来は、入力するデータに変形を加え、学習データを人工的に増やしてから深層学習に用いていました。一方、敵対的特徴生成では、深層ネットワーク内部で、認識が難しい苦手な特徴データを生成しながら学習します。入力するデータでなく、ネットワーク内部の数値に基づいて自動的に学習データを生成するため、多様なデータに対して汎用的かつ効率よく適用でき、専門家による調整が不要になりました（図9）。

3.3 実験

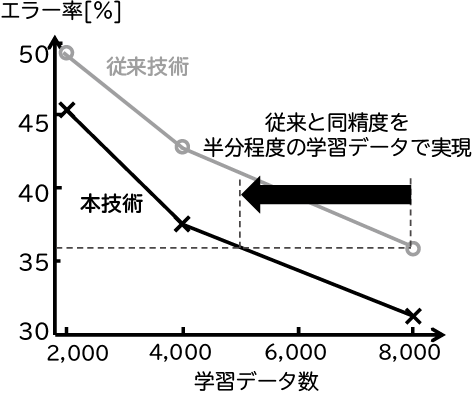
本技術の有効性を評価するため、手書き数字データMNISTと物体認識用データCIFAR-10を用いて実験を行い、従来のデータ拡張と本技術による認識精度を比較しました（図10、図11）。横軸は学習データ数、縦軸はテストデータに対するエラー率です。いずれも、本技術は従来手法に比べ低いエラー率を達成しており、従来と同精度を半分程度の学習データで実現していることが分かります。

4. むすび

本稿では、少量の学習データでも効率的な深層学習を行うために開発した2つの技術を紹介しました。層ごとの適応的正則化は、ネットワークの構造に応じて層ごとに異なる正則化係数を適切に設定でき、正則化が強すぎる層や弱すぎる層が混在する従来の課題を解決しました。敵対的特徴生成は、ネットワーク内部の数値に基づいて、認識が難しいデータを自動生成しながら学習するため、必ずしも精度改善に寄与するデータが作れないという従来の課題を解決しました。また、データ生成に関する専門家の調整も不要になりました。本技術により、大量の学習データを得ることが難しい実問題への深層学習の適用を可能とし、実用化をより一層加速させたいと考えています。

参考文献

執筆者プロフィール