Japan
サイト内の現在位置を表示しています。
グラフベース関係性学習(GraphAI)
人とともに未来を創る最新のAI技術私たちが取り扱う分析対象の多くはグラフで表現することができます。それらのグラフはデータポイントを表すノードと、さまざまな関係を表すエッジとで構成されています。例えば、ある患者の診断は、その患者のバイタルや人口統計学的情報だけではなく、患者の血縁者が持つ同様の情報、患者が訪れた病院に関する情報によっても特定が可能です。また、ある新事業の将来業績は、その企業のビジネス指標だけではなく、他の企業や人との関係、それらのネットワークや専門技能によっても予測できます。NEC欧州研究所と中央研究所の共同チームはこの洞察を更に押し進め、グラフで構成する世界をベースとしたグラフベース関係性学習(GraphAI)を追究することで、さまざまなビジネス領域で適用可能な画期的新技術を実現しました。この新技術は、ノード分類の性能を向上するだけでなく、リンク予測やグラフ分類のタスクを実現し、マルチモーダルでかつ不完全なデータソースを統合、更には複雑なAIモデルに「説明可能性」を与えることができます。
1. はじめに
現実世界における多様なビジネスアプリケーションに対して機械学習を適用しようとすると、多くの技術的課題に直面します。第一に、ラベリングされたデータを必要量入手することはしばしば困難です。例えば医療の領域においては、希少な医学上専門技能や、更にウェットラボ実験が必要となることもあるため、データポイントのラベリングのコストは高価になりがちです。第二に、解釈と説明の可能な機械学習方法を開発することが、これまで以上に重要になってきています。保険ビジネスを例に取れば、なぜある請求が不正であると機械学習法が予測するのかを説明し、更にはその予測に対する信頼性を把握できるようにすることが重要になります。第三に、画像・テキスト・時系列データなどの特徴量など、大量のセンサーからさまざまな属性値を持つデータが得られるわけですが、これらのデータモダリティのすべてを組み合わせて単一の機械学習モデルとするには、困難が伴います。欠損データの発生は当然この問題を悪化させることになりますが、医療及び金融を含むほとんどのビジネス領域では、欠損データは日常的に発生しています。最後に、AIビジネスが利益を得て拡張可能なものになるためには、どのようなユースケースにも対処可能で、更に他の用途においても再利用可能となる、堅固なデータ表現と処理フレームワークが必要です。
グラフベースの関係性学習は、問題領域を知識グラフとして表現することで前述の各課題に対応します。そのうえで、各領域特有の問題へのソリューションを算出するため、著者らが開発したグラフベースラーニングのフレームワークを得られたグラフに適用します。
本稿では、最初にグラフの意味と性質を紹介し、多くの問題がグラフで表現可能であることを提示します。次に、グラフベースラーニングの技術上の革新について説明します。この技術的革新こそが、グラフベースラーニングを競合する既存のアプローチと差別化します。最後に、顧客トライアルが実施された3つの具体的領域でのグラフベース関係性学習(GraphAI)の適用例について紹介します。
2. グラフベース関係性学習(GraphAI)
本章では、グラフの数学的概念に関連する必要な背景を紹介し、グラフベースの機械学習アルゴリズムの開発目的を説明します。また、さまざまな事例に適用する、NECが開発した学習フレームワークについても解説します。
2.1 背景と目的
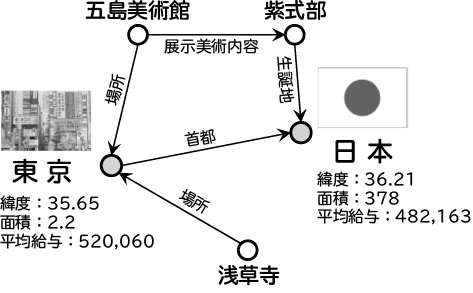
グラフは、ノードの集合とそれらノード間のエッジの集合で構成されています。通常、グラフのノードは、対象領域のデータポイントまたはエンティティを表しています。エッジは2個のエンティティ同士を接続しており、リレーションと呼ばれます。あるグラフに数種類のエッジが存在する場合、そのグラフはマルチリレーショナルグラフまたは知識グラフと呼ばれます。東京や日本などのエンティティに対応したノードと、エンティティ間に存在する場所や首都などの関係を表すエッジを持つ知識グラフを図1に示します。
多数の適用領域はグラフへのマッピングが可能です。例として、患者の集合とその患者の属性と患者間の類似性(左)と、化合物として表現したグラフ(右)を図2に示します。あるグラフ表現がアプリオリ(先験的)には存在しない場合であっても、多くの場合にはグラフを構築または学習することも可能です1)。例えば、適切に正規化が行われたリレーショナルデータベースから知識グラフ表現を構築することもできます。
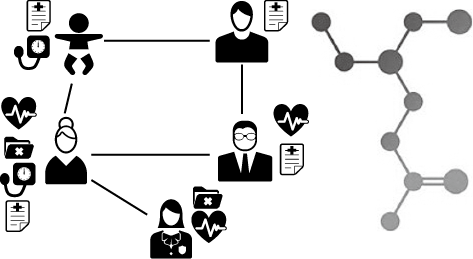
(右)化合物のグラフとしての表現
適用事例をグラフとして表現することで、グラフベース関係性学習(GraphAI)を適用して事例関連の予測クエリーに回答することが可能となります。例えば図2では、グラフ内のある患者について最も確率の高い診断を予測するために、グラフベースの学習を適用することができます。この予測は、当該患者が接続されている他のエンティティから決定的な影響を受けており、患者の属性のみを参考にするということはありません。
2.2 方法
グラフは本質的に3種類の予測問題に対応することが可能です。
ノード分類:グラフのノードのクラスラベルを予測すること。例としては、図2の患者の罹患している疾病の予測がある。この問題への入力は1個のグラフである。
リンク予測:グラフ内で失われたエッジを予測すること。例としては、顧客と製品をノードとして持つレコメンダーシステムで、ある顧客ノードと製品ノードを接続すべきかどうか予測したい場合がある。この問題への入力は1個のグラフである。
グラフ分類:あるグラフ全体のラベルを予測すること。例としては、図2に示す化合物が人間にとって有毒であるか判定する場合がある。この問題への入力は複数グラフの集合である。
グラフベースのリレーショナル学習は、これらの学習問題のすべてに適用可能なフレームワークです。用途にかかわらずグラフ内のノードやエッジはベクトル表現に変換されます。これらのベクトル表現はエンベッディング・ベクトル、あるいは組み込みベクトルと呼ばれます。グラフのエッジとノードがベクトルで表現することで、ディープラーニングによるエンドツーエンドの学習を適用することが可能になります。
以下、こうしたグラフベースのリレーショナル学習のフレームワークを構成する複数技術を説明します。
2.2.1 エンベッディングプロパゲーション
まず、エンベッディングプロパゲーション(EP)について説明します。ノードをカテゴリ分類することを目的とした技術で、そのためにグラフのノードをベクトル表現に変換します2)。EPにおける第一段階では、グラフのエッジ経由でメッセージを交換する「メッセージパッシング」という手法を用いて、個々の属性ごとにベクトル表現を学習します。ここで言う属性とは、例えば患者データからの学習というコンテキストにおいて、集中治療室の各患者について記録された時系列データがそれに当たります。EPにおける第二段階では、以前に学習した属性ごとのベクトル表現を組み合わせたノードごとのベクトル表現を学習します。そして、これらの組み合わせであるベクトル表現を、目的とする予測タスクに利用するのです。EPは、メッセージパッシングをベースとしたグラフのニューラルネットワークフレームワークの初めての試みであり、多くの半教師ありノード分類ベンチマークデータセットにおいて優れた精度を示しました2)。EPの利点は、各種、異なったデータモダリティ(ビジュアル、テキストなど)を組み合わせられることにあります。更には、欠損データのベクトル表現を明示的に学習することもできます。例えば、患者の転帰予測というコンテキストにおいては、EPは欠損データに対してロバストであり、同時に、予測転帰のために重要な特徴の判定が可能であり3)、これは医療領域においては決定的に重要となります。EPはまた、新抗原の発見という問題にも適用され、がんワクチンの開発に利用できるがんDNA内の突然変異の発見にも成功しています。
2.2.2 KBLRN:ナレッジベース・ラーナー
ナレッジベース・ラーナー(KBLRN)はリンク予測、つまり知識グラフ内の欠損エッジを予測するフレームワークです4)。KBLRNは関係性特徴量、潜在(学習)特徴量、数値特徴量といった複数の特徴量形式を統合・利用します。これらの特徴量は、多数または無限数の実数値を持つことができます。KBLRNが、2通りの方法でエンベッディングベース学習を確率論的モデルに統合することで、さまざまな特徴量形式の組み合わせが可能になります。第一の方法は、放射既定関数を備えた数値特徴のモデリングを行うことで、これらの特徴量形式のエンドツーエンドの可微分学習システムへの統合を可能にします。第二の方法では、確率論的エキスパート積(PoE)5)アプローチを用いて特徴量形式の組み合わせを行います。NEC欧州研究所と中央研究所の共同チームは、コントラスティブダイバージェンス法によるPoEトレーニングの代わりに、ネガティブサンプリング手法による分配関数の近似を実行しました。PoEアプローチには、共同したエンドツーエンドのフレームワーク学習が行えるという利点があります。図3で説明するように、どの関係においても、おのおの異なった特徴量形式を処理する別個のエキスパートが存在しています。そして、3つのサブモデル(潜在変数のエキスパート、関係性特徴量のエキスパート、数値特徴量のエキスパート)のスコアを加算して正規化しています。
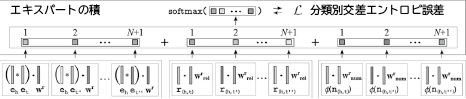
KBLRNの利点は、異なった特徴量刑式の組み合わせが実行できることです。これは、数値特徴量、関係性特徴量、潜在特徴量を組み合わせた初のナレッジベース学習アプローチです。KBLRNはベンチマークデータセットの集合においてより優れた精度を持つことが示されており4)、更には解釈可能なルール的特徴量の抽出も可能です。これらのルールをユーザーに提示することで、予測の説明を可能にします。
KBLRNは、パブリックセーフティや金融などの領域で適用されてきました。パブリックセーフティ領域では船舶の移動に関する質問への応答に利用され、金融領域では自動車保険請求が不正か否かの判別に利用されています。どちらのケースでも、重要なのは、予測できる、つまり事実に裏付けられた情報が不足していても推論できるということです。NECは更に、KBLRNを視覚的情報6)や時間的情報7)の作業も行えるように改良しました。
2.2.3 Patchy-SAN:グラフベースの畳み込みネットワーク
Patchy-SANはグラフ表現学習、つまりグラフのベクトル表現へのマッピングを行う学習関数のためのフレームワークです8)。これは主にグラフ分類問題に使用されます。画像用の畳み込みニューラルネットワークと同様に、Patchy-SANも、入力されたグラフからおのおののノード周囲の隣接関係を組み込みベクトルとして表現することができます。これらの隣接関係表現は効率的に生成され、畳み込みアーキテクチャの受容野として利用できます。その結果、効果的にグラフ表現を学習できるようになります。提案されたアプローチは、画像用の畳み込みニューラルネットワーク(CNN)9)から得られた概念のうえに築かれており、CNNを任意のグラフに拡張します。
このアプローチの長所は優れた効率性です。NECの実行時点において、最先端のグラフ分類アプローチであるグラフカーネルの性能を、処理速度と精度の両方において上回っていることが示されています。また、抽出したPatchy-SANの学習した構造特徴の視覚化も可能です。図4にその動作を示します。

フレームワークのグラフ分類問題への適用
Patchy-SANは、小規模な化合物分類などの生物医学領域の問題に適用され、最先端のアプローチを超える実績を挙げています。また、バイオメトリクスにおいては重要な問題であるグラフのマッチングに利用できるグラフ間の類似性算出にも利用可能です。
3. まとめ
NEC欧州研究所と中央研究所のメンバーで構成されるグループは、グラフベースの機械学習のための全般的フレームワークを開発しました。この技術は、現実世界のタスクをグラフ予測問題に構成することにより、広範囲なビジネス領域に対処できることを示しています。
4. 謝辞
NEC欧州研究所と中央研究所の山本風人氏、岡島穣氏、木村大地氏、その他のメンバーによる本プロジェクトの実施成功への貢献に感謝いたします。
参考文献
- 1)Luca Franceschi,Mathias Niepert,Massimiliano Pontil,Xiao He:Learning Discrete Structures for Graph Neural Networks,the 36th International Conference on Machine Learning (ICML)
- 2)Alberto Garcia-Duran and Mathias Niepert:Learning Graph Representations with Embedding Propagation,the 31st Annual Conference on Neural Information Processing Sys-tems (NIPS),2017
- 3)Brandon Malone,Alberto Garcia-Duran,and Mathias Niepert:Learning Representations of Missing Data for Predicting Patient Outcomes,2018
- 4)Alberto Garcia-Duran and Mathias Niepert:KBLRN: End-to-End Learning of Knowledge Base Representations with Latent, Relational, and Numerical Features,the 34th Confer-ence on Uncertainty in Artificial Intelligence (UAI)
- 5)G. E. Hinton:Training products of experts by minimizing contrastive divergence,Neural computation,Vol.14 Issue 8,pp.1,771–1,800,2002
- 6)Daniel Oñoro-Rubio,Mathias Niepert,Alberto García-Durán,Roberto González-Sánchez,Roberto J. López-Sastre:Answering Visual-Relational Queries in Web-Extracted Knowledge Graphs. In Proceedings of the 1st Conference on Automated Knowledge Base Construction (AKBC)
- 7)Alberto Garcia-Duran,Sebastijan Dumancic and Mathias Niepert:Learning Sequence Encoders for Temporal Knowledge Graph Completion,the Conference on Empirical Meth-ods in Natural Language Processing (EMNLP)
- 8)Mathias Niepert,Mohamed Ahmed and Konstantin Kutzkov:Learning Convolutional Neural Networks for Graphs,the 33rd International Conference on Machine Learning (ICML),2016
- 9)Fukushima Kunihiko:Neocognitron: A self-organizing neural network model for a mech-anism of pattern recognition unaffected by shift in position,Biological Cybernetics,Vol.36 Issue 4,pp.193–202,1980
執筆者プロフィール
Chief Researcher
NEC Laboratories Europe GmbH
Research Scientist
NEC Laboratories Europe GmbH
Ecole Polytechnique Fédérale de Lausanne
Senior Researcher
NEC Laboratories Europe GmbH
Senior Researcher
NEC Laboratories Europe GmbH
Deputy General Manager
NEC Laboratories Europe GmbH
セキュリティ研究所
主任研究員
セキュリティ研究所
研究部長
セキュリティ研究所
主任研究員
データサイエンス研究所
主席研究員
General Manager
NEC Laboratories Europe GmbH