Japan
サイト内の現在位置
NumPy互換数値演算ライブラリNLCPyの新機能SCAインターフェース
no.019ステンシル計算処理をベクトルエンジンで実施し高速化 サンプルコード「ライフシミュレーション」2022.6.201. NLCPy SCAインターフェース
引き続きNLCPy新機能の紹介です。2021年のバージョン2.0.0リリースに伴い、SCA (Stencil Code Accelerator)をPythonから使用するためのインターフェースが追加されました。NEC Numeric Library Collection で提供しているSCAの関数群をPythonスクリプトから容易に利用できるようにするためのものです。今回はステンシル計算サンプルプログラムによるSCAインターフェースの使用方法を紹介します。なおSCA は、画像処理や科学技術計算、ディープラーニングなどで頻出する処理パターンであるステンシル計算をベクトルエンジンで高速化するためのライブラリです。
2. ステンシル計算とは
ところで、ステンシル計算とはどのような処理でしょう。ステンシルは型版と訳されますが、特定のパターン（型版）に従って配列内の要素を更新していく処理を指します。また、フィルタリングなどの画像処理では近傍領域計算と呼ばれることがあります。
このステンシル計算は各種シミュレーションの中で多用されます。例えば、シミュレーションを実施する空間を定義してこれを格子状に分割します。その空間の中で時間経過とともに変化する何らかの物理的あるいはその他の状態を計算によって求めていくとき、空間は配列の形に置き換えられて、各格子点の情報は配列に収納されます。次に対象とする現象を熱方程式や波動方程式など常微分方程式で定義し、方程式を離散化することでステンシル（型版）を作っていきます。時間軸に沿って、このステンシルを使って空間内の各格子点の状態を意味する配列データを更新します。ここで方程式の離散化を行うことは、計算機処理のために何らかの形で近似することになります。この近似処理では差分法が多用されますが、差分法ではある空間内の格子点に対し、その近傍にある格子点が持つ情報をもとに何らかの漸化式に基づく計算によって更新します。そのため、差分法ではその内部でステンシル計算が行われているということができます。
ステンシル計算の応用分野は、流体解析、電磁界解析、分子動力学や量子力学の数値シミュレーションといった科学技術計算の分野だけではありません。例えば、金融デリバティブの価格付けに現れるブラックショールズ方程式を使用したオプションリスク指標シミュレーションがあります。また、平滑化、先鋭化、エッジ強調などの画像フィルタリング処理においてもステンシル処理が適用されることがあります。
3. SCAライブラリのステンシル形状とデータ定義
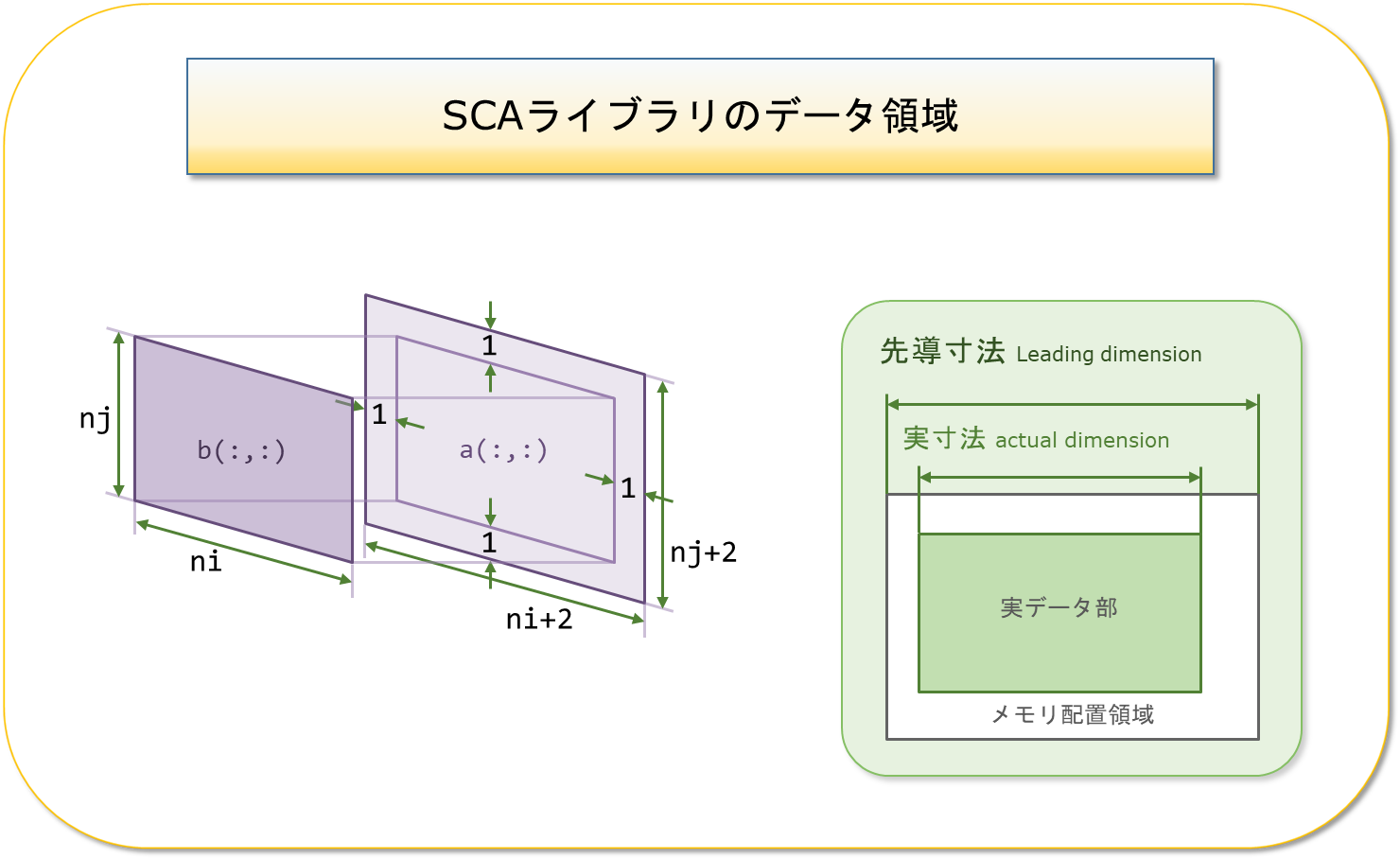
SCAインターフェースは4次元までの任意形状のステンシル形状を設定し計算することができます。1軸方向、平面、平面での2軸方向や対角方向、そして3次元や4次元の任意な方向においてステンシルの設定が行えます。また、ステンシルは任意の長さを選択することができます。SCAライブラリで処理する際のデータは、Figure-1のように実データに対して任意のサイズを縁取った領域がメモリに配置されます。
Figure-1
4. デモサンプルについて
常微分方程式や離散化、漸化式といった用語が頻出するシミュレーションですが、今回のサンプルはライフゲーム1と呼ばれる単純なルールに基づくシミュレーションゲームを使用して平易な例でSCAインターフェースの使い方を見ていきます。今回採用したライフゲームのルールについてはMathWorks 2にある説明の通りです。
サンプルプログラムで行う処理は次の通りです。初めに102x102の配列xinを用意した後に乱数で初期状態を作ります。ライフゲームでは疑似生命の生死を0または1で表現するため配列データは整数型で十分なのですが、SCAインターフェースは浮動小数点型データを扱うため、ここではfloat32を指定します。乱数により0.0または1.0の2値で配列を埋めることで疑似生命が生存する空間の初期状態の準備が完了します。
In [1]:
import nlcpy as vp
from matplotlib import pyplot as plt
from matplotlib import animation as anm
from IPython.display import HTML
In [2]:
my = 100; mx = 100; N= mx * my
DT = 'float32'
vp.random.seed(0)
xin = vp.zeros((my+2, mx+2), dtype=DT)
xin[1:-1, 1:-1] = vp.random.randint(0, 2, N).reshape(my, mx)
print(xin)
[[0. 0. 0. ... 0. 0. 0.] [0. 0. 1. ... 1. 1. 0.] [0. 1. 1. ... 0. 0. 0.] ... [0. 0. 0. ... 0. 1. 0.] [0. 0. 1. ... 0. 1. 0.] [0. 0. 0. ... 0. 0. 0.]]
In [3]:
xout = vp.zeros_like(xin)
dxin, dxout = vp.sca.create_descriptor((xin, xout))
desc_i = (dxin[-1,-1]+dxin[-1,0]+dxin[0,-1]+dxin[1,1]+dxin[1,0]+dxin[0,1]+
dxin[-1,1]+dxin[1,-1])
desc_o = dxout[0]
sca_kernel = vp.sca.create_kernel(desc_i, desc_o=desc_o)
In [4]:
fig, ax = plt.subplots(figsize=(6, 6))
ims = []
ims.append([plt.imshow(xin[1:-1, 1:-1], cmap="summer")])
for i in range(100):
res = sca_kernel.execute() # Execution of Kernel
xin[:,:] = (xin.astype(vp.int) & (res == 2)) | (res == 3) # updates
im = ax.imshow(xin[1:-1, 1:-1], cmap="summer")
ims.append([im])
ani = anm.ArtistAnimation(fig, ims)
html = HTML(ani.to_jshtml(fps=2))
plt.clf()
html
Out[4]:
<Figure size 432x432 with 0 Axes>
In [ ]:
続いてステンシル計算のためのオブジェクトdxin, dxoutを定義します。この際、sca.create_descriptorに事前に作成したxinとxoutを入力しています。desc_iにステンシル計算の内容を定義します。このステンシル計算は2次元空間のある点を中心として上下左右と斜め隣の計8の配列内に生存(1.0であるもの)する疑似生命数を合算するものです。このdesc_iと出力先であるdxoutを入力値としてcreate_kernelによってカーネルsca_kernelを定義します。使用するステンシル記述定義式をFigure-2示します。
Figure-2
メイン処理であるループ（今回は100回、これは疑似生命の100世代分をシミュレート）内で先に定義したカーネルsca_kernelを呼び出すことでステンシル計算処理します。結果はresに引き渡されますが、このresには周囲に存在する生物数が保存されています。resの値（疑似生物の生存数）が2であると同時にその位置に生存しているとき、または合計値3であるときに次世代での生存を許すものとして、xinをアップデートします。なお、先に定義したカーネルsca_kernelは繰り返し再利用することで処理負担を軽減しています。また、xinのアップデートではスライス:を使用して同一のメモリアドレスに情報が更新されるようにしています。これによって、カーネル作成時に指定したxinと同じメモリアドレスに新しいデータが毎回格納されるために、ループ内においてカーネルを再利用したステンシル計算が可能となります。
5. その他SCAライブラリを使用した計算サンプル
今回のサンプルでは前後左右斜めの計8要素を足し合わせる単純なステンシル計算でしたが、科学技術計算や画像フィルターでは係数を使ったより複雑な処理が行われます。NLCPyユーザーズガイドに熱拡散解析、波動解析や流体解析といった
サンプルプログラムが用意されていますのでご覧ください。
関連リンク
最新資料／カタログはこちらからダウンロード
ご紹介資料、各種カタログをダウンロードいただけます。
My NEC登録が必要です
My NEC登録が必要です
