Japan
サイト内の現在位置
山崎 大のコラム
運命の人と出会うのは明日かも?~独身男性の統計学~

NEC AI・アナリティクス事業部
山崎 大
2019年1月23日
はじめに
私は普段、流通・小売業のお客様を中心にデータ分析をしております。統計学とマーケティングの関係は強く、最近ではAIを利用して次の日の商品需要量を予測して、自動で最適量を発注するシステムも珍しくありません。「区間推定」は商品の知名度アンケートを取った際に、よく使われる手法で、アンケート結果から全体(アンケートをとっていない人も含む)の回答を推定することができます。今回は生活の中での区間推定の応用例を紹介します。
区間推定
区間推定とは「母集団の母数(パラメータ)に対して、その母数を仮定したとき観測されるデータの『95パーセント予言的中区間』に現実に観測されたデータが入るような母数だけを集める推定の方法」です。
難しく説明しておりますが、簡単に言うと、無作為に抽出したサンプル(=標本)のデータから、全体のデータの平均値を求める方法です。
この手法を適用している有名な例の1つが選挙速報です。
選挙である候補者Aの投票率Rを推定する方法は以下になります。
- 投票用紙全体からn枚をランダムに抽出する
- 抽出したn枚の内、候補者Aの名前が書かれている枚数をaとし、その比率をrとする(r=a/n)
この時、Rは信頼度95%で
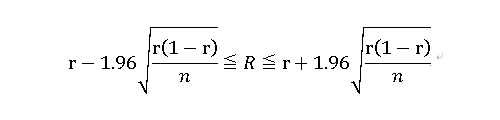
が成り立つ。
例えば、
- 投票用紙全体から10,000枚をランダムに抽出
- 抽出した10,000枚の内、候補者Aの名前が書かれている枚数が6,000枚
だった場合、比率は r=6000/10000=0.6 となるので、
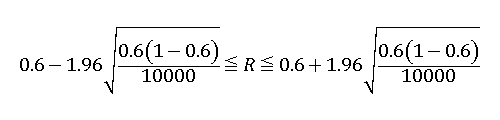
となり、0.59≦R≦0.61(信頼度95%)ということがわかります。これはつまり
「95%の確率で候補者Aの投票率が59%~61%になる」
ということを示しております。この「信頼度95%」や「1.96」がどこから来たかについては参考文献の「完全独習 統計学入門」を見て頂けばと思います。
もし全投票数が100,000枚だった場合、開票率1%で候補者Aが過半数を獲得できる可能性が高いと推定できます。
運命の人と出会う確率の推定
少し難しい話が続いてしまったのですが、「無作為に抽出したデータで全体の平均が求まる」ということをご理解頂けば、一旦大丈夫です。この理論を応用して、運命の人に出会う確率を推定してみましょう。独身の方、必見です!
前提条件は下記になります。
- 確率を求めるのはAさん30歳、独身男性、現在彼女なし
- これまでに出会った女性の中で、理想の人と思えたのは7人(内3人とはお付き合い)
- 30年の人生の中で、100ヵ月を無作為に抽出(n=100)
- 抽出100ヵ月の内、理想の人と出会えた月は5ヵ月(同じ理想の人の重複ありとした場合、a=5)
比率は r=5/100=0.05 となるので、0.007≦R≦0.093(信頼度95%)となりました。
つまりAさんの30年の歴史の中で0.7%から9.3%の割合で理想の人と出会っていることになります。期間に直すと2.6ヵ月から33.4ヵ月となります。
現在、理想の人に出会えていない場合、少なくとも2.6ヵ月の期間は出会える可能性が95%の確率であるということになりますね!
注意
実はこの結果は本来考慮すべき点を全て無視して計算しており、正確な値ではありません。
- 理想の人を見逃しているかも
今回Aさんの理想の人を主観で選んでいますが、この「理想の人」の定義が曖昧となっています。もしかしたら駅ですれ違った人が実は理想の人だったかもしれないし、生まれてまもなくで、まだ物心ついていない時に会った人が理想の人だったかもしれないので、その方々をカウントしなければなりません。 - 出会える環境が異なる
30年の人生を基に今後の30年を推定しましたが、学生時代は共学で女性が多く、職場は男性ばかりで出会いが少ない可能性を考慮しておりません。今回の検証はAさんの環境の男女比率が常に一定という条件を含んでおります。
最後に
理想の人の定義や環境など、たくさん考慮すべき点がありますが、いかがでしたでしょうか?統計を勉強していると難しい言葉ばかりで敬遠してしまいがちでありますが、自分のこれまでのデータに照らし合わせてみると意外と身近に感じるかもしれません。ちなみに筆者は現在独身で、あえて年齢は書きませんが、確率は0ではないことだけはわかりました。この記事を読んでいる運命の人、明日にでも出会って頂ければ幸いです。
参考文献
参考文献:小島寛之(2006)「完全独習 統計学入門」ダイヤモンド社
